Giới thiệu

Nói một cách ngắn gọn, Vector space model (Mô hình không gian vector) là một mô hình đại số (algebraic model) thể hiện thông tin văn bản như một vector, các phần tử của vector này thể hiện mức độ quan trọng của một từ và cả sự xuất hiện hay không xuất hiện (Bag of words) của nó trong một tài liệu.

Mô hình này biểu diễn văn bản như những điểm trong không gian Euclid n-chiều, mỗi chiều tương ứng với một từ trong tập hợp các từ. Phần tử thứ i, là di của vector văn bản cho biết số lần mà từ thứ i xuất hiện trong văn bản. Sự tương đồng của hai văn bản được định nghĩa là khoảng cách giữa các điểm, hoặc là góc giữa những vector trong không gian.

Mỗi từ trong không gian vector sẽ có một trọng số, có nhiều phương pháp xếp hạng khác nhau, nhưng tf-idf (term frequency–inverse document frequency) là một phương pháp phổ biến để đánh giá và xếp hạng một từ trong một tài liệu. MySQL fulltext search cũng sử dụng phương pháp này. Về cơ bản thì tf-idf là một kỹ thuật (cụ thể là ranking function) giúp chuyển đổi thông tin dưới dạng văn bản thành một Vector space model thông qua các trọng số. Vector space model và tf-idf được phát triển bởi Gerard Salton vào đầu thập niên 1960s.

Mặc dù đơn giản, nhưng mô hình không gian vector và những biến thể của nó hiện nay vẫn là cách phổ biến để biểu diễn văn bản trong Data mining và Information retrieval. Tuy nhiên, một trong những điểm yếu của vector space model số chiều lớn (high-dimensonal), có khoảng cỡ chục triệu chiều trong không gian vector nếu như chúng ta áp dụng nó vào web search engine.

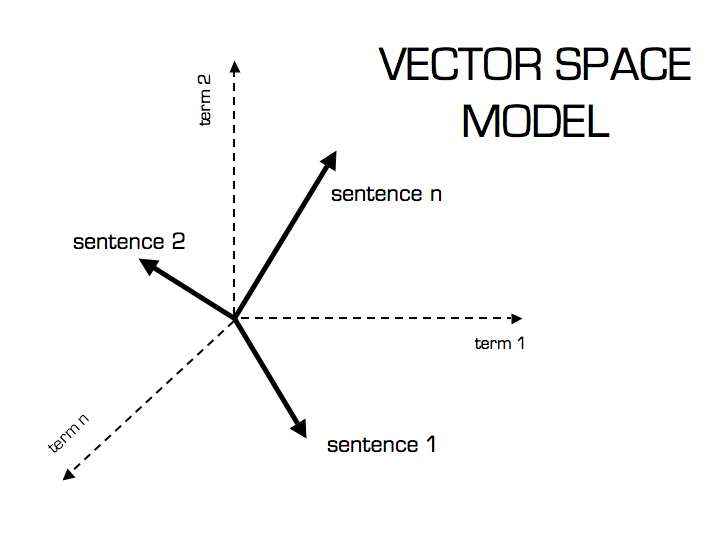Hình minh họa của Christian S. Perone Hình minh họa của Christian S. Perone

Thể hiện văn bản như vector và term frequency

Ví dụ: Hàng đầu tiên là danh sách các vở kịch của Shakespeare. Cột đầu tiên là các từ, và các ô thể hiện sự xuất hiện hay không xuất hiện của các từ đó trong các tác phẩm.

  Anthony and Cleopatra Julius Caesar The Tempest Hamlet Othello Macbeth
Anthony 1 1 0 0 0 1
Brutus 1 1 0 1 0 0
Caesar 1 1 0 1 0 1
Calpurnia 0 1 0 0 1 0
Cleopatra 1 0 0 0 0 0
Mercy 1 0 1 1 1 1
Worser 1 0 1 1 1 0

Binary incidence matrix (Introduction to Information Retrieval)

Và mỗi tài liệu được biễu diễn dưới dạng một vector, ví dụ Julius Caesar \(\left[\begin{matrix} 1 \\ 1 \\ 1 \\1 \\0 \\0 \\0 \end{matrix}\right]\)

Các ô thể hiện sự số lần xuất hiện của các từ trong các tác phẩm. Nó được gọi là term frequency.

  Anthony and Cleopatra Julius Caesar The Tempest Hamlet Othello Macbeth
Anthony 157 73 0 0 0 1
Brutus 4 157 0 2 0 0
Caesar 232 227 0 2 0 1
Calpurnia 0 19 0 0 1 0
Cleopatra 57 0 0 0 0 0
Mercy 2 0 3 8 5 8
Worser 2 0 1 1 1 0

Và mỗi tài liệu được biễu diễn dưới dạng một vector, ví dụ Julius Caesar \(\left[\begin{matrix} 73 \\ 157 \\ 227 \\19 \\0 \\0 \\0 \end{matrix}\right]\)

Bây giờ mỗi tài liệu (trong trường hợp này là tác phẩm) được thể hiện dưới dạng một vector đếm.

Term frequency tft,d xác định số lần từ t xuất hiện trong tài liệu d. Nhưng chỉ tần suất xuất hiện của một từ thôi thì chưa đủ.

Ví dụ trong một tài liệu, sự xuất hiện của một từ 10 lần thì tài liệu đó được coi là phù hợp hơn tài liệu mà từ đó chỉ xuất hiện 1 lần. Nhưng không phải là phù hợp hơn tài liệu kia 10 lần. Sự phù hợp không tỷ lệ thuận với số lần xuất hiện của từ đó trong một tài liệu.

Phương pháp tính trọng số tần suất logarit (log-frequency)

Log-frequency của một term t trong document d được tính như sau: \(w_{t,d} = 1 + \log(tf_{t,d})\)

Nếu \(tf_{t,d} > 0\), nếu không thì \(w_{t,d} = 0\)

Nếu từ đó không xuất hiện trong một tài liệu, thì tft,d bằng 0. Và bởi vì log(0) là một số âm vô cùng, cho nên chúng ta phải cộng 1.

Một từ xuất hiện trong tài liệu: 1 lần có w=1 2 lần w=1.3 10 lần w=2 1000 lần w=4

Điểm cho một cặp document-query được tính bằng tổng của các trọng số của term \(t\) trong cả document \(d\) và query \(q\) = \(\sum_{t\in q \cap d }({1 + \log(tf_{t,d})})\) Điểm sẽ bằng 0 nếu như query terms không xuất hiện trong document

Phương pháp tính trọng số nghịch đảo văn bản (Inverse document weighting)

Từ hiếm thì quan trọng hơn những từ có tần suất xuất hiện cao. Trong mỗi ngôn ngữ có những từ lặp đi lặp lại nhiều lần nhưng vô nghĩa (ví dụ trong tiếng Anh là a, the, to, of v.v), trong full-text search nó được gọi là stopwords.

Đối với term frequency, thì những từ càng xuất hiện nhiều thì có điểm càng cao, còn những từ hiếm thì điểm xếp hạng lại thấp hơn. Do đó chúng ta cần một cách đánh giá khác với các từ hiếm, vì nó sẽ mang nhiều thông tin hơn là những từ phổ biến trong văn bản.

Ví dụ trong một tập hợp các tài liệu về nghành công nghiệp ô-tô, thì từ khóa “ô-tô” sẽ có khả năng có mặt hầu hết trong tất cả các tài liệu. Để hạn chế nhược điểm này, người ta giới thiệu cơ chế để giảm thiểu sự ảnh hưởng của việc này và tăng tính chính xác khi quyết định sự phù hợp của tài document và query. Ý tưởng là giảm trọng số của từ nào có document frequency cao, bằng cách lấy tổng số tài liệu (N) chia cho số tài liệu mà một từ xuất hiện.

Nếu gọi dft là số văn bản chứa một term t thì dft là cách đánh giá ngược sự hữu ích của t. ( dft bé hơn N → số tài liệu trong tập hợp mà chúng ta có).

Chúng ta định nghĩa trọng số idf của một từ t bởi: \(idf_t = \log_{10} (N/df_t)\)

Chúng ta sử dụng log10(N/dft) thay vì N/dft để giảm tác dụng ảnh hưởng của idf, như đã nói ở trên do số lần một từ xuất hiện nhiều lần thì không có nghĩa là nó quan trọng về ngữ nghĩa.

Trong MySQL người ta thay thế bằng \(\log_{10} ((N-nf/nf)\)

(Xem thêm về MySQL)

Ảnh hưởng của idf trên việc xếp hạng

idf không có ảnh hưởng trên việc xếp hạng tài liệu (so với 1 từ khóa), nó chỉ giúp phân loại tài liệu. idf chỉ có ảnh hưởng lên sự xếp hạng các tài liệu nếu như query có ít nhất 2 terms. Ví dụ người dùng search từ khóa “capricious person”, idf làm cho sự xuất hiện của từ capricious được tính nhiều hơn trong kết quả xếp hạng tài liệu cuối cùng, so với từ “person” vì từ này phổ biến hơn.

Collection và Document frequency

term dtf idft
calpurnia 1 log(1000000/1)=6
animal 100 log(1000000/100)=4
sunday 1,000 3
fly 10,000 2
under 100,000 1
the 1,000,000 0

Collection frequency của từ t là số lần xuất hiện của t trong tập hợp các tài liệu. Một ví dụ về idf, giả sử N=1,000,000. Mỗi một từ trong tập hợp sẽ có một giá trị idf tương ứng. Còn document frequency biểu diễn số document trong collection chứa một term t nào đó.

Câu truy vấn cũng được xem như một vector

Để tìm một cụm từ trong tập hợp các tài liệu sẵn có (giống khi thực hiện một câu truy vấn full-text), thì chúng ta cần so sánh cụm từ đó (query) với các tài liệu sẵn có. Ý tưởng là chúng ta cũng xem các câu truy vấn như là một vector (xem ở trên), và chúng ta sẽ xếp hạng (rank) các tài liệu mà chúng ta có dựa vào sự tương đồng (proximity) với câu truy vấn (query).

Để xếp hạng các tài liệu mà chúng ta có (và trả về các tài liệu có hạng cao), thì chúng ta so sánh câu truy vấn với tập hợp tài liệu. Tài liệu nào càng gần với câu truy vấn thì có điểm cao hơn.

Để so sánh hai vector chúng ta có thể tính khoảng cách giữa hai vector, hoặc tính góc tạo ra bởi hai vector. Tuy nhiên cách tính khoảng cách có nhược điểm không chính xác, bởi vì khoảng cách lớn với các vector có chiều dài khác nhau (ví dụ: tài liệu d′ là nhân đôi nội dung tài liệu d).

Khoảng cách Euclid giữa \(\vec q\) và \(\vec d\) 2 là rất lớn ngay cả khi sự phân phối của các từ trong query q và trong tài liệu d2 là rất giống nhau.

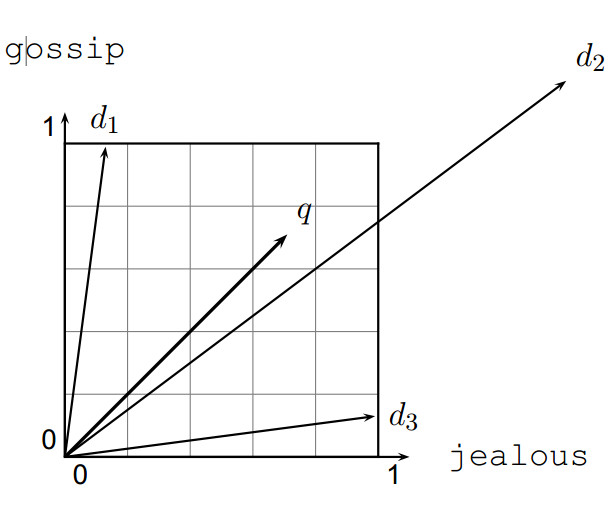
Khoảng cách Euclid

Nhìn hình trên ta có thể thấy khoảng cách giữa \(\vec q\) và \(\vec d\) 2 là khá lớn mặc dù sự phân bố các terms trong query q và document d2 khá tương đồng.

Do vậy chúng ta sẽ dựa vào GÓC trong không gian vector hơn là khoảng cách giữa cách điểm.

Sử dụng góc thay vì khoảng cách

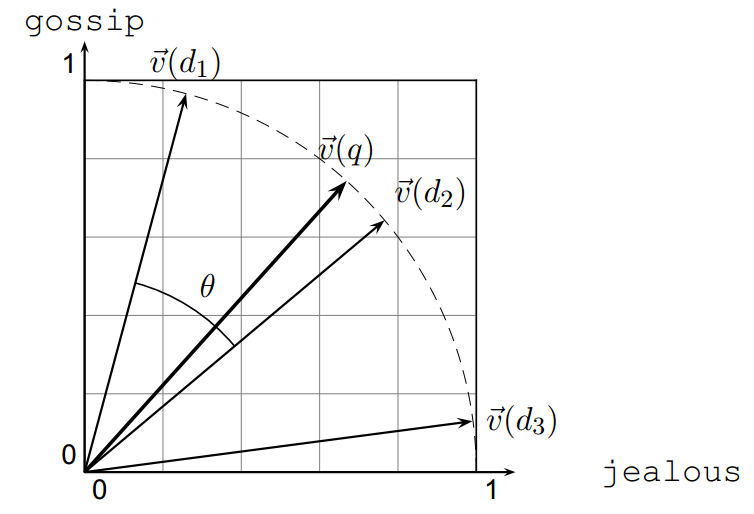
Sử dụng góc

Qua thực nghiệm, lấy một tài liệu d và gắn vào chính nó, ta có tài liệu d’ . Về mặt ngữ nghĩa thì hai tài liệu này hoàn toàn giống nhau về nội dung. Khi đó vector d’ sẽ có độ lớn gấp đôi vector d và có cùng chiều với d.

Nhưng khoảng cách Euclid giữa hai tài liệu này khá lớn, mặc dù giống nhau về nội dung.

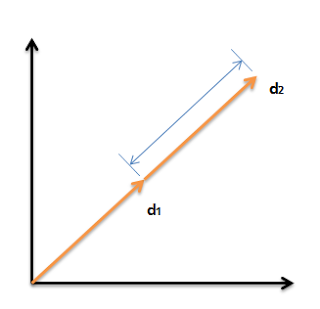
Khoảng cách euclid

Cho nên, thay vì xếp hạng tài liệu dựa trên khoảng cách Euclid, thì chúng ta nên xếp hạng dựa trên góc giữa tài liệu và câu truy vấn.

Ta có thể thấy góc giữa hai vector càng lớn thì cosin hay điểm xếp hạng sẽ càng thấp. Khi góc giữa vector bằng 0 thì điểm sẽ lớn nhất (=1).

Có hai cách ghi tương đương nhau:

  • Xếp hạng tài liệu theo thứ tự giảm dần dựa trên góc giữa query và document
  • Xếp hạng tài liệu theo thứ tự tăng dần dựa trên cosin của query và document

Cos curve

Tài liệu được xếp hạng bởi giá trị cosine giảm dần:

  • cos(d,q) = 1 khi d = q
  • cos(d,q) = 0 khi tài liệu d và query q không có bất kỳ từ chung nào.

Tại sao phải chuẩn hóa độ dài của tài liệu?

Với cái tài liệu dài (hơn): Tài liệu dài có tần suất các từ xuất hiện cao hơn (higher term frequencies). Một từ giống nhau sẽ có khả năng xuất hiện thường xuyên hơn. Có nhiều từ hơn, tăng khả năng xuất hiện của các từ trùng với câu truy vấn.

Sự “chuẩn hóa cosine” giảm sự ảnh hưởng của tài liệu dài (so với tài liệu ngắn). Một vector có thể được chuẩn hóa (về độ dài) bằng cách chia từng phần tử của nó cho độ dài của nó. Để tính độ dài của vector chúng ta làm như sau (định mức L2 hay L2 norm):

\[\mid\mid\vec x\mid\mid=\sqrt{\sum_i{x^2_i}}\]

Giả sử chúng ta có vector d \(\left[\begin{matrix} 3 \\ 4 \end{matrix}\right] → \sqrt{\sum{x^2}} = \sqrt{3^2 + 4^2}=5\)

Giả sử chúng ta có vector d’ \(\left[\begin{matrix} 6 \\ 8 \end{matrix}\right] → \sqrt{\sum{x^2}} = \sqrt{6^2 + 8^2}=10\)

Chia một vector cho định mức L2 của nó sẽ tạo ra một vector đơn vị chiều dài (unit length vector)

Khoảng cách euclid

Khoảng cách Euclid giữa hai vector là khá lớn (trong khi góc bằng nhau). Sau khi chuẩn hóa hai tài liệu d và d’chúng ta có hai vector hoàn toàn giống nhau \(\left[\begin{matrix} 0.6 \\ 0.8 \end{matrix}\right]\). Những tài liệu dài và ngắn bây giờ (sau khi chuẩn hóa) sẽ có trọng số so sánh được.

Mặc dù vậy cách chuẩn hóa này vẫn chưa đúng hoàn toàn, cho nên người ta còn giới thiệu thêm phương pháp “pivoted document length normalization”.

Tương đồng Cosine (cosine similarity)

\[cos(\vec q, \vec d)= \dfrac{\vec q, \vec d}{\mid\vec q\mid \mid\vec d\mid} = \dfrac{\vec q}{\mid\vec q\mid} . \dfrac{\vec d}{\mid\vec d\mid} = \dfrac{\sum_{i=1}^{\mid v \mid} q_i d_i}{\sqrt{\sum_{i=1}^{\mid v \mid} q^2_i} \sqrt{\sum_{i=1}^{\mid v \mid} d^2_i}}\]

\(q_i\) là trọng số tf-idf của từ i trong câu truy vấn. \(d_i\) là là trọng số tf-idf của từ i trong tài liệu \(cos(\vec q, \vec d)\) là sự tương đồng cosine giữa \(\vec q\) và \(\vec d\) hay là cosine của góc giữa \(\vec q\) và \(\vec d\)

Đối với những vector đã được chuẩn hóa về độ dài, sự tương đồng cosine chỉ đơn giản là tích vô hướng của hai vector (scalar product).

\(cos(\vec q, \vec d) = \vec q . \vec d = \sum_{i=1}^{\mid v \mid} q_i d_i\) \(\quad\quad \text{for q,d length-normalized}\)

Còn về vấn đề hiện thực hóa những kỹ thuật và lý thuyết ở trên thành code như thế nào thì chúng ta có thể tham khảo thêm bài viết sau: Short Introduction to Vecto Space Model

References: